【中１理科・数学】食塩水問題を克服！〜方程式演習編①〜食塩の量に着目して解こう！
![【中１理科】“食塩水”の攻略[方程式演習編]](https://mana-brain.com/wp-content/uploads/2020/10/shokuen-02-2.jpg)
みなさんこんにちは！
今回は、中学1年生理科「食塩水」の方程式演習編①です。
まずは解説を見る前に、こちらの対策プリントを自分の力で解いてみましょう。
▼下の画像をクリックして実際に問題を解いてみよう！▼
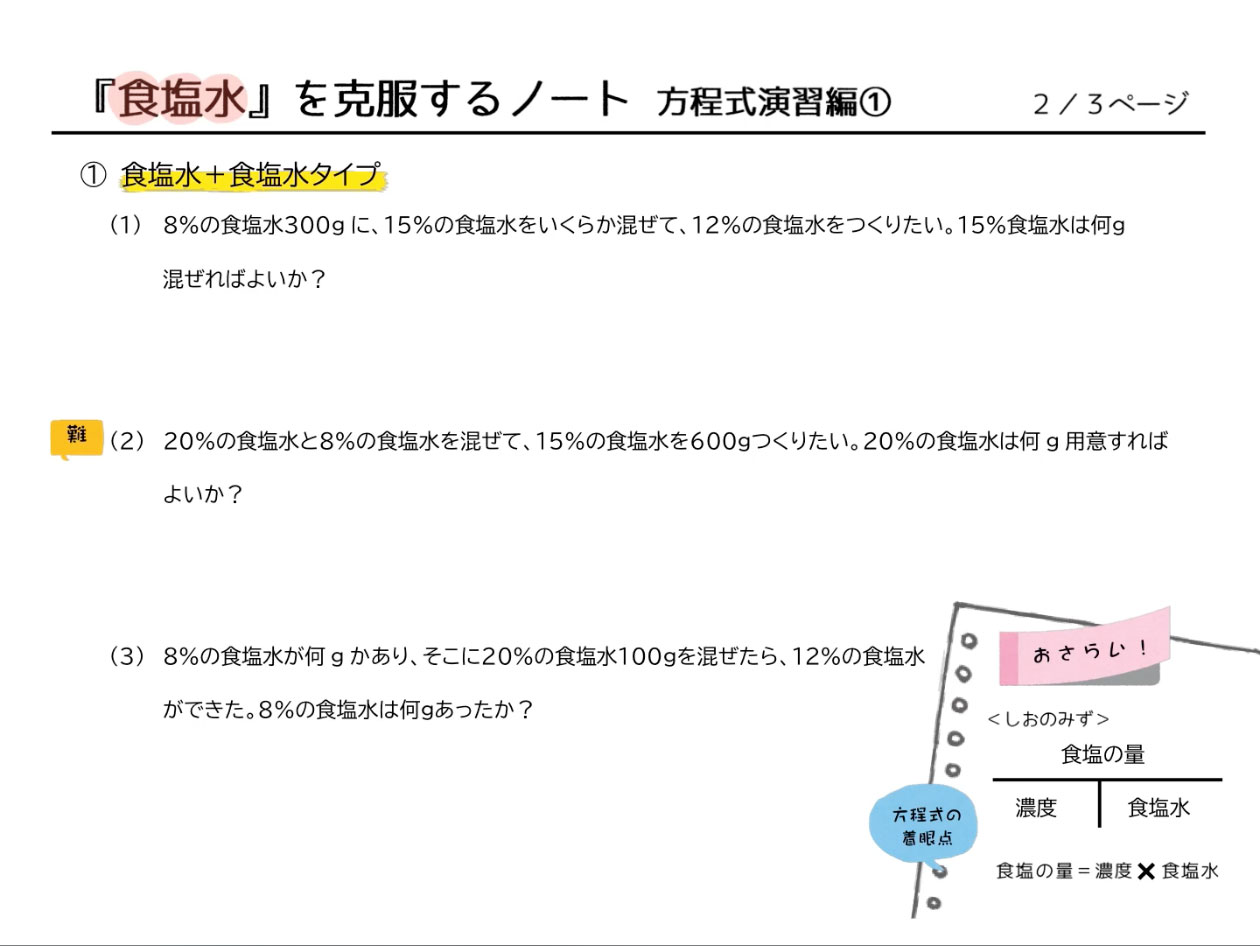
今回のポイントは【方程式は食塩の量に着目して解いていくのが基本パターン】ということです。
▼第一弾はこちら
https://mana-brain.com/post-4061/本サイトでご紹介しているような講義を実際に受けてみませんか？お子様の学習相談などもお気軽にお近くの校舎までお問い合わせください。
動画で答えと解説を確認！
それではここから解説に入ります。解説はアニメーション動画で行っています。
▼下の動画をクリックして解説を聞きましょう▼
（ここからは動画の6:06までをテキストで解説したものになります）
みなさんこんにちは。
今回は食塩水を克服するノートを作る第二弾です。方程式の演習編に入ります。
今回は食塩水に食塩水そのものを混ぜるタイプの問題です。
問題(1)解説
8%の食塩水300gに15%の食塩水をいくらか混ぜて、12%の食塩水を作りたい。15%食塩水は何g混ぜればいいですか？
ポイントは【食塩の量】でした。
濃度を分数で表して、食塩水の量とかけることでの量が計算できますね。
方程式は食塩の量に着目して解いていくのが基本パターンです。
8%の食塩水300gなので、300×8/100=24gですね。
次に15%の食塩水の量は謎なので Xg と置きましょう。
すると、この食塩水の中の食塩の量は X×15/100=0.15x となります。
そして合わさった食塩水は 300g+Xg なので、(300+X)×12/100 という式で合計した食塩水の中に含まれる食塩の量が出せますよね。計算して、36+0.12X まで解いてください。
ここで方程式が作れます。
24+0.15Xは、8%と15%の食塩水に含まれていた食塩を合計したという意味ですね。
=36+0.12X
これは混ぜてできた12%食塩水に含まれる食塩の量。そして二つの混ぜ合わせた食塩水に含まれる食塩の量と一致するはずですね。
これを解くと0.03X=12となり、X=400
すなわち、15%食塩水は400gと答えが出るわけですね
わかりましたか？
結局は、「混ぜ合わせる食塩水の中に入っている食塩+食塩=出来上がった食塩水に含まれる食塩」という食塩の量に注目した方程式を作れば解けるという仕組みですね
問題(2)解説
では２番です。これはちょっと難しいですよ。
20%の食塩水と8%の食塩水を混ぜて15%の食塩水を600g作りたい。20%の食塩水は何g用意すればいいですか？
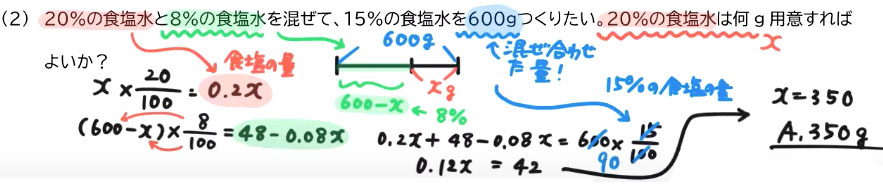
先ほどと同様に、「食塩の量」に着目した方程式を作ります。
20%食塩水は量が分からないので、Xgとしましょう。
すると、X×20/100=0.2X となりますね。
この0.2Xも食塩の量です。
そして混ぜ合わせた結果、600gになるんですから、8%の食塩水の量は、引き算で出すことができますよね。
すなわち、600-X。これが8%食塩水の量になりますよね。
そうすると食塩の量は、
(600-X)×8/100=48-0.08X となりますね。
分配法則大丈夫ですね？
この二つの食塩の量を合計すると、15%・600gの食塩水の食塩の量と一致するはずです。
これを解くと、X=350と出ます。
20%食塩水は、350g用意すれば良い、と分かりました。
どうでしょうついてきますか？
問題(3)解説
どんどん行きましょう。（３）です。
8%の食塩水が何gかあり、そこに20%の食塩水100gを混ぜたら12%の食塩水ができました。8%の食塩水は何gありましたか？
これはさっきの問題を入れ替えて作っただけなので、さくっと解けますよね。
式はこうなります。
X×8/100=0.08X
それと
100×20/100=20
合わせて
(X+100)×12/100=0.12X+12
これらの食塩の量を使って方程式を作ると、
0.08X+20=0.12X+12
これを解くと
X=200
これが答えになりますね。
実際に自分で解いたノートと見比べてみてくださいね！
さて、３問解きましたが、前回のものも含めて同じパターンで解いていますが慣れてきましたか？
手順は基本的に同じなので、まずは慣れてくださいね。
では、次の動画では方程式演習編②をやっていきましょう。
お子様の勉強や受験、英会話にお悩みではないですか？
こんなお悩み、ありませんか？
私たちにお任せください！
全国約100校舎を展開する「めんどうみ」が自慢の学習塾/個別指導塾です
![中1理科 “食塩水”の攻略[理論編] 動画で解説](https://mana-brain.com/wp-content/uploads/2020/07/shokuensui.jpg)
